Exploring the Stability of Permanent Magnets
Permanent magnets play a pivotal role as sources of a consistent magnetic field within specific confines. Their stability is of utmost importance for precision instruments and magnetic devices, as it directly correlates with the accuracy and reliability of these tools. However, various external factors, such as temperature fluctuations, time, electromagnetic fields, mechanical disturbances, radiation, and chemical reactions, can influence the performance of these magnets.
Key Changes in Magnetic Performance
- Magnetic Domain Structure Alterations: Commonly referred to as magnetic aging, these changes are reversible. When the magnet undergoes re-magnetization, most of its properties can be restored.
- Microstructural Modifications: Known as structural aging, these changes are irreversible. Even with re-magnetization, the magnet’s original properties remain altered.
Factors Influencing Magnet Stability
The stability of a magnet encompasses several aspects:
- Temperature Stability: How the magnet’s performance parameters change with every 1°C temperature increase.
- Time Stability: The annual decay of residual magnetism at room temperature.
- Vibration and Shock Stability: Especially relevant for magnets used in spacecrafts.
- Electromagnetic Field and Chemical Stability: Essential for magnets operating in acidic or alkaline environments or under high humidity.
Depending on the environment in which a magnet operates, different stability performances are required. For instance:
Spacecraft Magnets: These magnets are typically concerned with stability under vibrations and impacts. They also need to remain stable under radiation, temperature fluctuations, and over time.
Magnets in Harsh Environments: Magnets that function in acidic or alkaline settings, or in environments with high humidity (like in steamy heat or salt mists), generally need to exhibit strong chemical stability.
Magnets in Varying Temperatures: In areas where the operational temperature is not constant, it’s vital to ensure that the magnet maintains its temperature stability.
Temperature Stability in Permanent Magnets
Temperature Impact on Magnet Performance
Devices crafted from magnetic materials often operate under fluctuating temperatures. Such environmental temperature changes can directly impact the magnet’s performance. To ensure these devices function optimally amidst temperature variations, it’s crucial to understand the magnet’s performance shifts with temperature.
Several temperature stability parameters have been defined to quantitatively represent the effects of temperature on magnet performance. These include:
- Residual Magnetism Temperature Coefficient (\(α_{Br}\))
- Intrinsic Coercivity Temperature Coefficient (\(α_{HcJ}\))
- Reversible and Irreversible Losses in Open-Circuit Magnetic Flux Density
Notably, \(α_{Br}\) and \(α_{HcJ}\) are among the critical performance indicators for commercial permanent magnets. These coefficients represent the relative change rate of a physical quantity with temperature. For instance, a positive \(α_{Br}\) indicates an increase in residual magnetism with rising temperature, while a negative value signifies a decrease.
Residual Magnetism Temperature Coefficient & Intrinsic Coercivity Temperature Coefficient
Temperature coefficients, as the name suggests, represent the relative rate of change of a physical quantity with temperature. Specifically, from a reference temperature, \(T_0\), to a higher temperature, \(T\), the definitions for the residual magnetism temperature coefficient and the intrinsic coercivity temperature coefficient are given, with units in %/℃.
\[α_{Br} (T)=\frac {B_r(T)-B_r(T_0)}{(T-T_0) \cdot B_r(T_0)} \times 100\%\]
\[α_{HcJ} (T)=\frac {H_{cJ}(T)-H_{cJ}(T_0)}{(T-T_0) \cdot H_{cJ}(T_0)} \times 100\%\]
In this context, \(B_r(T)\) and \(B_r(T_0)\) denote the residual magnetism at temperatures \(T\) and the reference temperature point \(T_0\), respectively (the same applies for \(H_{cJ}\)). Typically, room temperature or 20℃ is chosen as \(T_0\). The value for the higher temperature, \(T\), is determined based on the operating environment and is agreed upon by both the supplier and the user. If \(α_{Br}\) is positive, it indicates that the residual magnetism increases with a rise in temperature. Conversely, if it’s negative, the residual magnetism decreases as the temperature goes up.
Reference Standards
The sintered neodymium iron boron permanent magnets have national standards (GB/T13560-2017) that provide reference values for various grades of permanent magnets in terms of residual magnetism temperature coefficient and intrinsic coercivity temperature coefficient.
Temperature coefficients | Material Type | Temperature Range | Unit | Value |
Residual Magnetism Temperature Coefficient | N type | 20°C~100°C | %/°C | −0.090~−0.124 |
M type | 20°C~100°C | %/°C | −0.090~−0.124 | |
H type | 20°C~100°C | %/°C | −0.090~−0.124 | |
SH type | 20°C~100°C | %/°C | −0.090~−0.122 | |
SH type | 20°C~150°C | %/°C | −0.095~−0.124 | |
UH type | 20°C~100°C | %/°C | −0.090~−0.120 | |
UH type | 20°C~180°C | %/°C | −0.095~−0.122 | |
EH type | 20°C~100°C | %/°C | −0.090~−0.120 | |
EH type | 20°C~200°C | %/°C | −0.095~−0.122 | |
TH type | 20°C~100°C | %/°C | −0.095~−0.122 | |
TH type | 20°C~200°C | %/°C | −0.095~−0.122 | |
Intrinsic Coercivity Temperature Coefficient | N type | 20°C~100°C | %/°C | −0.70~−0.82 |
M type | 20°C~100°C | %/°C | −0.65~−0.80 | |
H type | 20°C~100°C | %/°C | −0.60~−0.75 | |
SH type | 20°C~100°C | %/°C | −0.55~−0.70 | |
SH type | 20°C~150°C | %/°C | −0.50~−0.65 | |
UH type | 20°C~100°C | %/°C | −0.50~−0.62 | |
UH type | 20°C~180°C | %/°C | −0.48~−0.61 | |
EH type | 20°C~100°C | %/°C | −0.50~−0.62 | |
EH type | 20°C~200°C | %/°C | −0.46~−0.58 | |
TH type | 20°C~100°C | %/°C | −0.47~−0.58 | |
TH type | 20°C~200°C | %/°C | −0.45~−0.623 | |
Curie Temp. | – | K | 583~623 | |
Demag. Coeff. | – | – | 1.05 | |
Reversible Temperature Coefficient
Magnets typically operate in an open-circuit state with an air gap. The characteristics of open-circuit residual magnetism (or open-circuit magnetic flux) changing with temperature are of practical significance. When the environmental temperature rises from room temperature \(T_0\) to a given temperature \(T_1\), the open-circuit magnetic flux drops from \(B(T_0)\) to \(B(T_1)\). If the temperature returns to room temperature \(T_0\), the open-circuit magnetic flux generally recovers to a value slightly lower than \(B(T_0)\), as illustrated in graphs below. Experiments have shown that when the temperature fluctuates between \(T_0\) and \(T_1\), and the temperature difference ΔT is not very large, the change in B is linearly reversible.
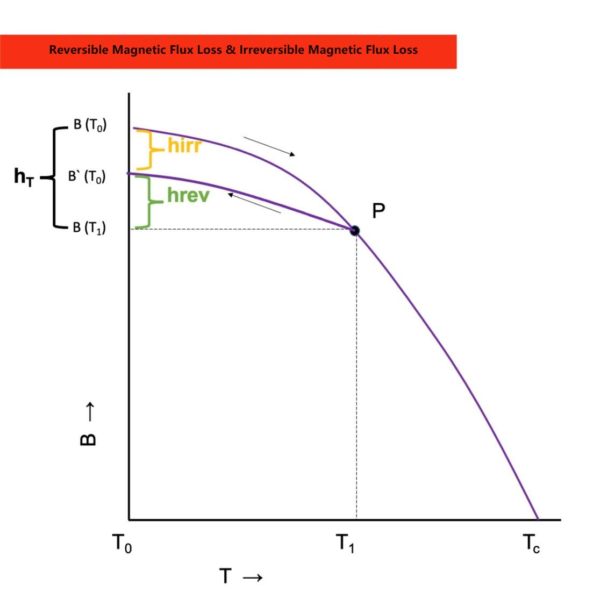
\[\overline{α}=\frac {B(T_1)-B`(T_0)}{(T_1-T_0) \cdot B`(T_0)} \times 100\%\]
During the entire heating process, the total magnetic flux loss from room temperature to high temperature is represented by \(h_T\). It can be decomposed into two parts: the reversible magnetic flux loss and the irreversible magnetic flux loss. From certain graphs, it’s evident that when the temperature varies within the range of \(T_0\) to \(T_1\), the change in B is linear. The average reversible loss of open-circuit magnetic flux is represented by the reversible temperature coefficient α.
Within the broader concept of temperature coefficients, it’s essential to differentiate between the general temperature coefficient, the reversible temperature coefficient, and the irreversible temperature coefficient. Each of these terms has distinct implications, and understanding their nuances is crucial.
Aging treatments play a pivotal role in enhancing the stability of permanent magnets. Such treatments can significantly reduce parameters like \(h_T\), \(h_{Irr}\), \(h_{Rev}\), and \(α\). Before a permanent magnet is used or tested, it undergoes an aging process, where it’s heated to a specific temperature for a set duration. This process helps eliminate any unstable structures within the magnet. The temperature and duration for the aging treatment are determined based on the magnet’s type, intended use, and other relevant factors.
The reversible temperature coefficient \(αB (T)\) or the residual magnetism temperature coefficient \(α_{Br} (T)\) is influenced by the material’s intrinsic magnetism. By introducing specific elements, one can alter the relationship between the saturation magnetization strength of the main magnetic phase and temperature, thereby modifying the magnet’s temperature coefficient. For instance, in neodymium-iron-boron (NdFeB) magnets, partially replacing Fe with Co can significantly elevate the Curie temperature of the primary phase. Similarly, substituting some Nd with Dy can improve \(αB (T)\).
