Introduction
The question of whether magnets of identical performance and volume have the same pulling force is a common one. Online sources claim that neodymium-iron-boron (NdFeB) magnets can lift 640 times their weight, but is this reliable information?
This query leads us to explore what factors influence a magnet’s pulling force. It’s crucial to recognize that magnets only attract ferromagnetic materials, such as iron, cobalt, nickel, and their alloys, and have no effect on non-ferromagnetic materials.
Online formulas for calculating magnetic force include:
\[F=kB^2S/2\]
\[F=0.577SB^2\]
Are these formulas accurate? While not precise, they correctly suggest that a magnet’s pulling force is related to the magnetic field strength (B) and the contact area (S). The larger these factors, the stronger the pulling force.
Shape and Magnetic Force
Considering magnets of equal volume but different shapes—flat, cylindrical, and elongated—do they exert the same pulling force?

The answer is no. The shape significantly impacts the magnetic force, with the optimum being when a magnet operates near its maximum energy product point, meaning it can perform the most work.
Here’s something to keep in mind, for maximum pulling force, the attracted object must be large enough to cover the magnetic poles entirely, eliminating material, size, or shape from affecting the force.
Optimal Shape for Maximum Pulling Force
To determine if a magnet is at its most efficient working point, consider the magnet’s attraction state. For a cylindrical magnet, when the height to diameter ratio (H/D) is approximately 0.6, it achieves maximum pulling force. This rationale supports why magnets are often designed in relatively flat shapes for use as attachments. For instance, an N35 10 mm dia x 6 mm Thickness magnet, through FEA simulation, is shown to have a pulling force of about 27N, nearly 780 times its weight, showcasing the maximum potential for magnets of similar volume.
Similar principles apply to square and cylindrical magnets when directly attached to an attracted material. At the center, Pc≈1, indicating operation near the maximum energy product point, maximizing the pulling force for the given volume.
The Impact of Multi-Pole Magnetization
It’s important to note that the above discussion primarily pertains to magnets in a single-pole magnetization state. However, the scenario changes drastically when considering multi-pole magnetization. The pulling force in a multi-pole magnetized state can significantly exceed that of a single-pole magnetization, especially when the object being attracted is in close proximity.
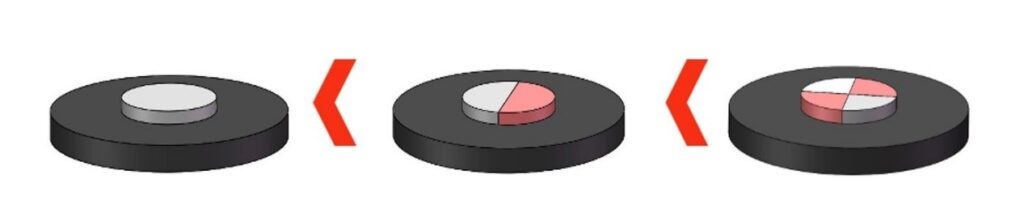
Why Multi-Pole Magnetization Increases Pulling Force?
The reason for the substantial increase in pulling force with multi-pole magnetization, even when the volume of the magnet remains constant, is the unchanged contact area (S), coupled with a significant increase in the magnetic flux density (B) through the attracted object. This effect is vividly demonstrated in magnetic flux line diagrams, where the density of lines passing through a piece of iron from a multi-pole magnetized body is markedly higher. Taking an N35 10 mm dia x 6 mm thickenss magnet as an example, converting it to a dual-pole magnetization through FEA simulation shows that its pulling force on an iron plate can reach about 1100 times its weight.
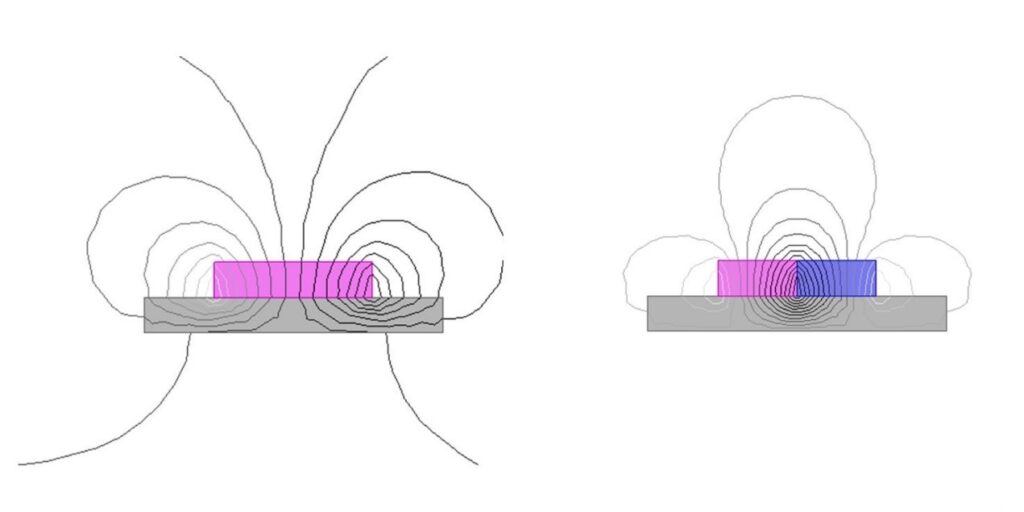
After a magnet is multi-pole magnetized, each pole behaves as if it were a longer, thinner magnet, altering its optimal Pc value. Therefore, the ideal dimensions for a multi-pole magnetized magnet no longer adhere to the H/D≈0.6 guideline but shift towards a flatter shape. The specific dimensions optimal for a multi-pole magnet depend on the magnetization method and the number of poles involved.
This intricate relationship between magnetization patterns and pulling force underscores the complexity of magnetic interactions and the engineering precision required to optimize magnet performance for specific applications.
Conclusion
Magnetic attraction is a complex phenomenon influenced by material composition, magnet shape, and magnetization pattern. Understanding these variables allows us to debunk myths about magnetic force and appreciate the engineering behind optimizing magnets for various applications. This exploration reveals that while two magnets may share volume and material, their pulling force can vary dramatically based on shape and magnetization, highlighting the intricate balance between physical properties and magnetic performance.
